PRISE case study

Introduction of the case study

The subject of our research is a safety function, designed to initiate an emergency prevention action in the occurrence of the so-called PRISE event. This safety function is used in the Paks Nuclear Power Plant (Paks NPP) located in Hungary. Nuclear power plants are highly safety-critical and complex systems, where the correct operation of the safety procedures is of great importance. The plant protection systems must satisfy high safety requirements and minimize spurious forced outages. Therefore, formal modelling and verification methods need to be applied to prove the correctness and completeness of the PRISE safety function.
 

The PRImary-to-SEcondary leaking (PRISE) event is one of the major faults in a reactor unit, resulting due to a non-compensable leaking of parts in the primary circuit. The PRISE event occurs when there is a rupture or other leakage within the steam generator (SG) vessel primary tubing, affecting either a few (3-10) tubes or their collector that contain the high-pressure activated liquid of the primary circuit.

In the unlikely case of a PRISE event, the safety procedures first initiate the emergency shutdown (scram, trip) of the reactor, and then isolate the faulty steam generator. However, there would still be a possibility to release some of the contaminated water to the environment, if the event would not be handled properly. In order to prevent this and to increase the safety of the plant, a safety valve for draining the contaminated water into the containment has been added to each steam generator, and a new safety function, the PRISE safety function has been developed to control its operation.

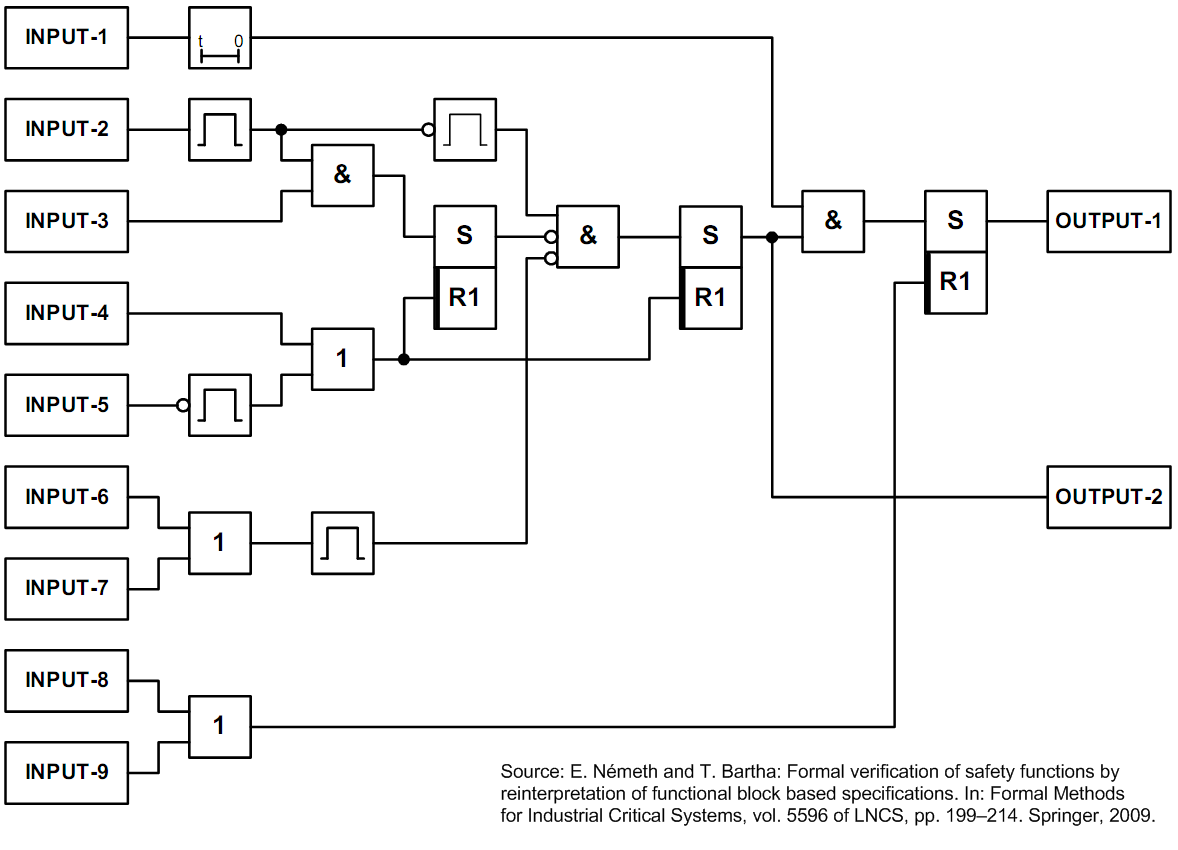
The PRISE safety function FBD is shown in the following figure:

The purpose of the PRISE safety function is to initiate the draining of the steam generator if and only if a PRISE event occurs. This implies preventing the activation of the safety valve, when a non-PRISE fault event (causing similar symptoms, but without a classified PRISE event)
occurs, i. e., the PRISE safety function must be selective. Moreover, when the reactor unit is either being started up or shut down, thus it is not in the normal operating regime, the PRISE safety function is designed not to be active. In these circumstances the operators can activate
the draining valve manually, should a need arise.

Modelling

We have created a hierarchical Coloured Petri net model of the PRISE safety function. Next figure shows the high-level main net of our CPN model. The gray circles are the inputs and outputs of the PRISE logic. The larger labelled rectangles are substitution transitions that denote subnets of the corresponding function blocks. The smaller net elements are simple places and transitions that are only needed for connecting the subnets. This main net integrates and connects the separately developed and validated lower-level CPN subnets of the different functional
blocks. The transformation of the Functional Block Diagram was straightforward and simple to validate, since the structure of the FBD graph and the corresponding CPN graph are isomorphic.

Verification of the PRISE safety function

Our aim was to prove that the PRISE safety function initiates the draining always if a PRISE event occurs in every normal operation regime coupled with a fault in the SG level sensor that is highly unreliable; and never if a PRISE event does not occur even if severe faults causing similar symptoms happen. In addition, it is also important to prove that the PRISE detection logic is free from deadlocks as they represent dangerous situations. The required selective detection of the PRISE event, and the heuristic design process of the safety logic made it necessary to perform a rigorous formal verification of the PRISE safety procedure.

The verification process consisted of three main steps:

1. Development of the model and formalisation of the requirements
2. State space exploration and storage
3. Evaluation of the temporal logic expressions, proving the requirements

Formalization of the requirements

We could translate the above requirements into the following verification goals:

• Liveness requirement: the secondary water draining activity is always activated when a real PRISE accident has occurred (no actuation masking).
• Safety requirement: the draining activity is not activated if not a real PRISE accident has occurred (no erroneous actuation).
• Deadlock freeness: No deadlock situation can arise for any combination and sequence of input signals.

We used branching-time temporal logic based model checking to prove the requirements. For complexity reasons we chose CTL temporal logic, as it provides an expressive formalism with efficient decision procedures.

• First, we checked the deadlock freeness of the system. Informally this means that in every state there exists at least one reachable successor state. The equivalent CTL temporal logic expression is the following: AG(EX(true))}.
• We also checked if the model is reversible, that is from every state we can reach the initial state. We expressed it with the following CTL formula: AG(EF(init)). This property ensures that the safety function can be made ready to fulfil its purpose in all circumstances.
• We used indirect proof to prove the safety requirement. We transformed the inverse requirement into the following CTL formula: E([!(PRISE-event)] U [actuation]). This formula is satisfied only if the draining activity is activated without a PRISE event.
• The liveness requirement was also easier to prove by indirect proof. We formalised the inverse requirement as the following CTL expression: EF(PRISE-event AND EG(!(actuation) AND !(reset-event))). Informally, we are searching  for strongly connected components in the state space that contain no actuation and reset-event, but contain a PRISE-event.

Evaluation of the temporal expressions

The next step of the verification was to explore and store the state space of the CPN model of the PRISE safety function, using our coloured saturation algorithm and state space storage data structures. After obtaining the complete state space we could evaluate the four CTL expressions. For state space traversal and temporal logic based model checking we used the analysis modules of the PetriDotNet framework. Our measurements can be found in [1].

Reference:

[1] Tamás Bartha, András Vörös, Attila Jámbor, Dániel Darvas: Verification of an Industrial Safety Function Using Coloured Petri Nets and Model Checking. In: 14th International Conference on Modern Information Technology in the Innovation Processes of the Industrial Entreprises (MITIP 2012), pp. 472-485, Budapest, Hungary, 10/2012.